Games202-lecture8-全局光照（屏幕空间）

大纲

预计把上节课没有讲的LPV和VXGI将完，然后把SSAO和SSDO介绍完

LPV（Light Propagation Volumes）

LPV最早是在孤岛危机3（”显卡危机”）中被引入的

关键问题

思考：每个Shading Point能够查询到每个方向来的环境光照，Radiance在传播过程中不会改变

LPV的想法就是把场景体素化为多个voxel，然后预计算每个格子获取的直接Radiance，然后再传播到其它voxel中

做法的步骤

1. 生成场景直接的radiance

2. 注入到体素化的voxel中

3. 计算Radiance传播后的Radiance

4. 渲染时查询voxel直接使用

具体一点的步骤

step1: 先生成场景直接的Radiance

可以用RSM加速

step2:把直接Radiance注入到格子中

场景的体素化可以预计算划分好，把格子包括的虚拟点光源的Radiance储存起来（这里应该会根据法线等使用不同的brdf），格子里面储存的是一个2阶的球谐系数来模拟各个方向的Radiance分布

step3:在格子中传播Radiance直到收敛（这里一般不考虑visibility，不然太难了）

每次把格子中的radiance往隔壁的6个面中去传播

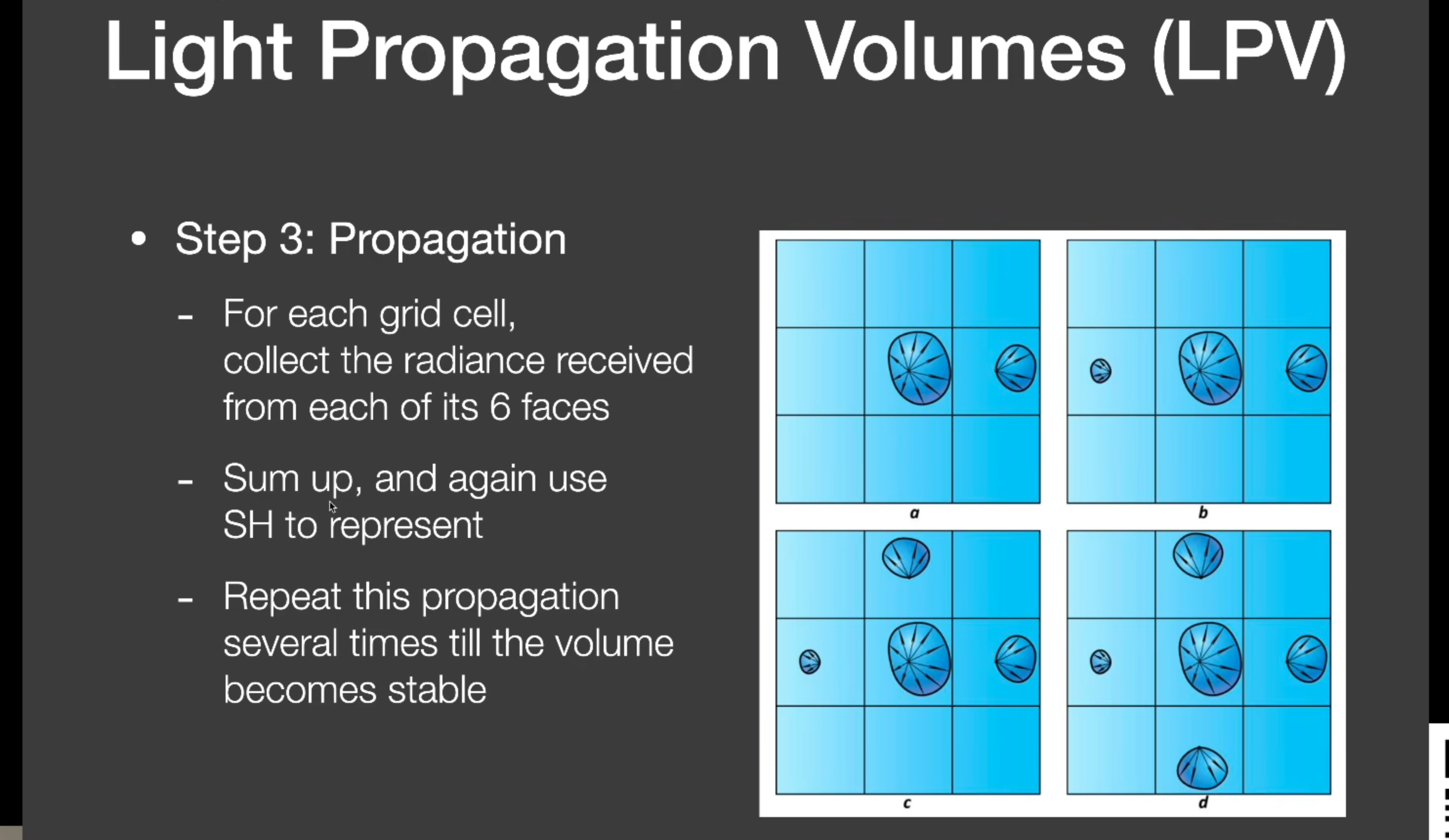
step4:用Shading Point所属格子中SH来还原光照渲染，问题
（格子粒度大了薄一点的墙壁会漏光，可以用八叉树等来加速）

VXGI （Voxel Global Illumination）

执行两趟的算法，与RSM比较：VXGI会体素化场景，RSM是表面像素；VXGI在Shading Point用Cone Tracing来追踪体素的Radiance，RSM的Shading Point对每个光源的RSM的像素计算Radiance

VXGI需要体素化这个场景，并把场景用八叉树来管理

步骤

step1:
每个体素记录对应表面的法线分布，还需要记录光源incident的分布，然后再简历树状结构（可能是把低级的voxel记录的值平均一下）

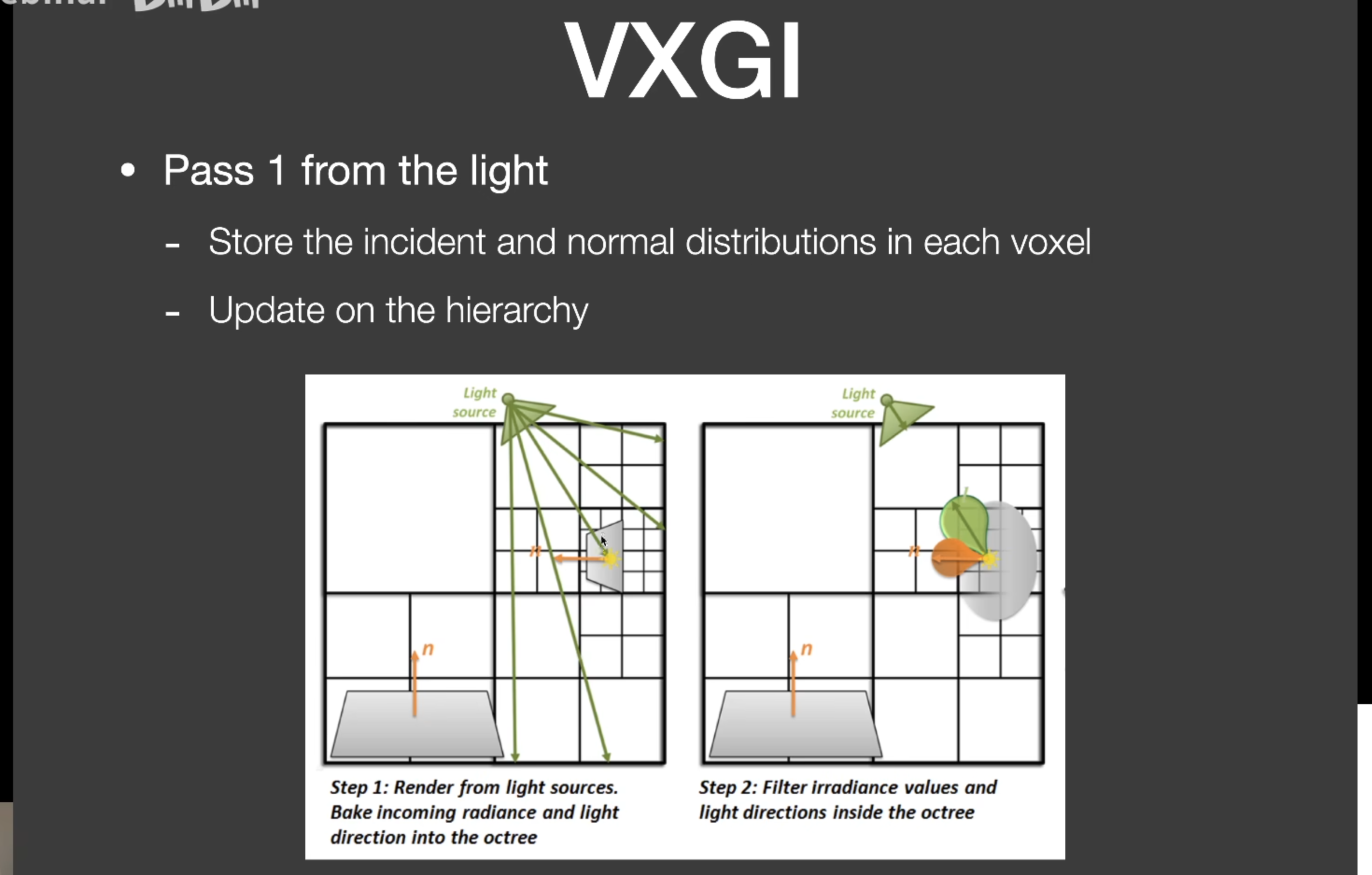
step2: 用Cone
Tracing来查询Radiance，用树状的Voxel来加速（锥形越远会越大，查询的体素Level也需要更高），

对于Glossy表面，只在反射方向发射一个Cone就行了，例子上查4次就可以累加出Radiance了

对于Diffuse表面，用8个小圆锥查询，然后加起来就好了（闫神说也可以用一个巨大圆锥），缝隙和覆盖问题这里不严格考虑

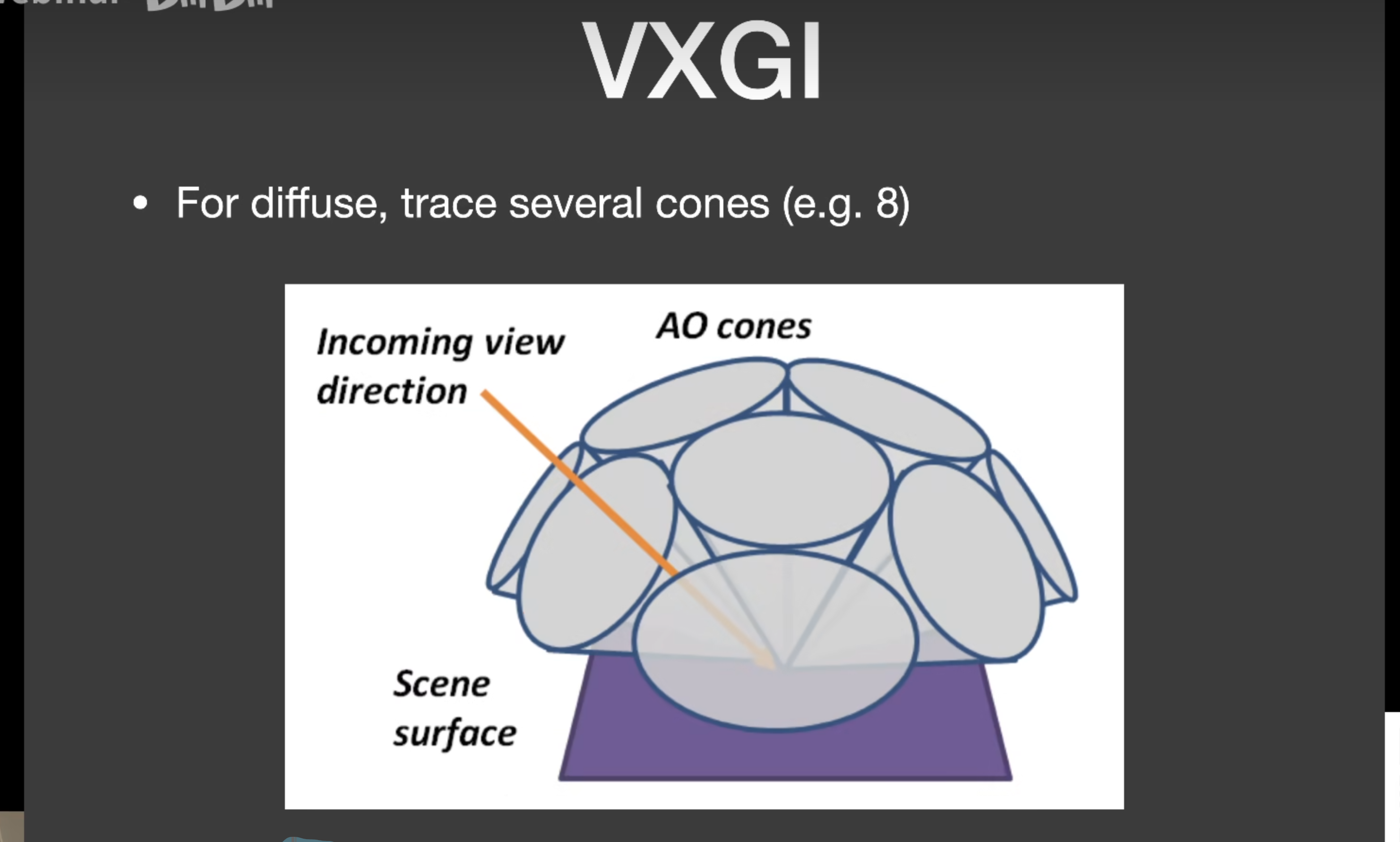
VXGI于LPV相比：

1. VXGI比LPV慢

2. VXGI比LPV效果更好一些，因为VXGI是追踪BRDF方向的，而LPV不考虑遮挡让光源传播出来的

3. 都需要体素化，VXGI需要的精度可能更高，而且需要建立层级结构

屏幕空间环境光遮蔽（SSAO）

引入SSAO

ssao最早在Crytek引擎引入

AO会在物体接触位置生成一些阴影，看起来会更加有立体感（而且AO相对来说好实现）

SSAO是对环境光照的部分信息的近似，所有的信息来源是屏幕空间。SSAO做了两个假设，一是不知道间接光照的来源，二是假设环境光是常数

SSAO考虑到不同方向对环境光的可见性不一样，并且把所有材质在AO上都假设为Diffuse材质

SSAO的原理

从下面的图考虑环境光的假设（可能跟BRDF的G项类似，越复杂的地方光线越难进来或者出去）

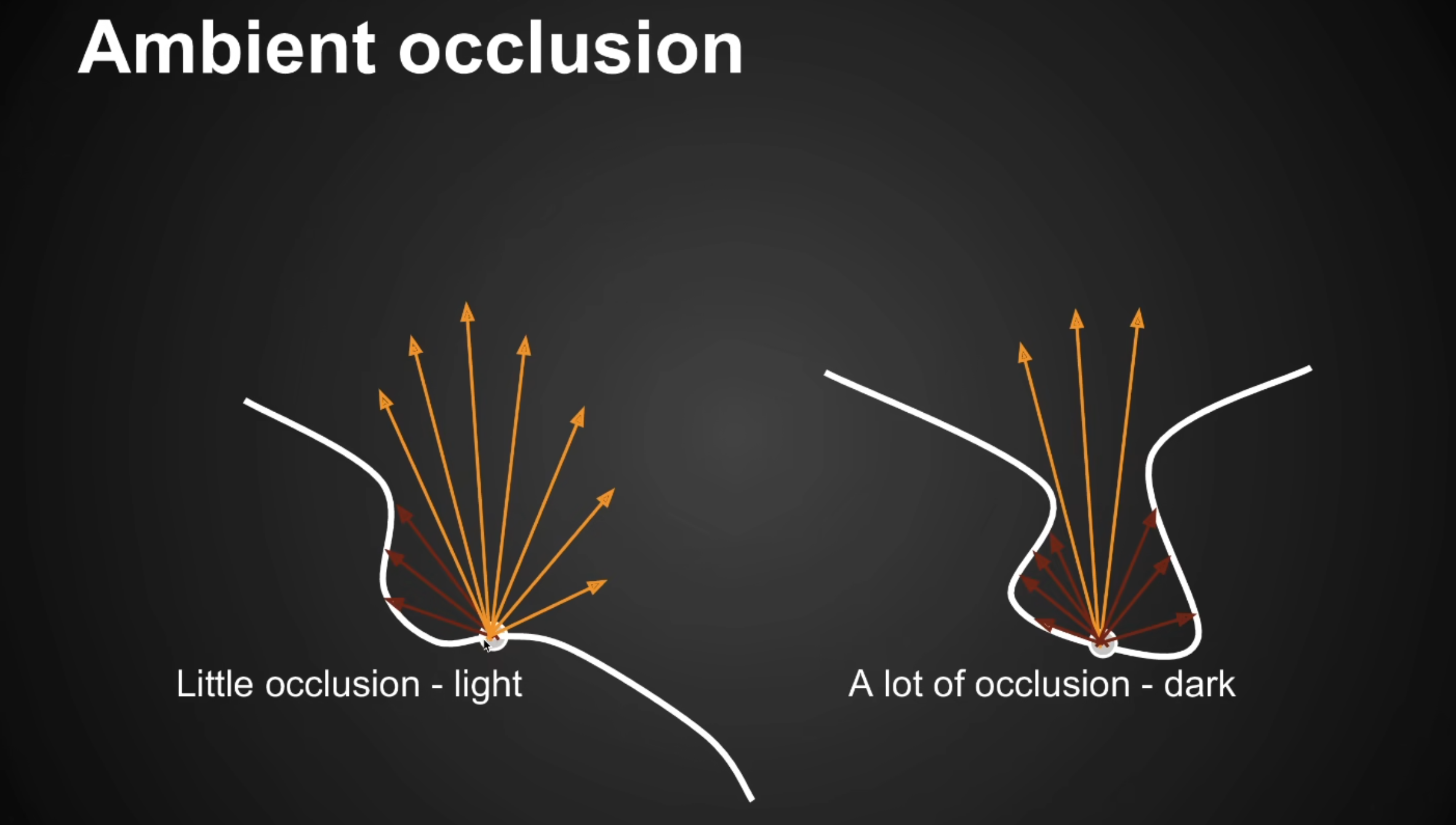
从渲染方程来考虑SSAO的背后的原理。把可见性拆分出来，积分出来的值相当于Ka，光照部分就相当于常数的Albedo

更深的理解积分拆分后，对前面的积分相当于是在积分域内对f(x)求平均

更深的理解，为啥篮筐位置的下面会有个cosθ。因为光照方程可以看成对cosθdwi积分，而不是对dwi积分

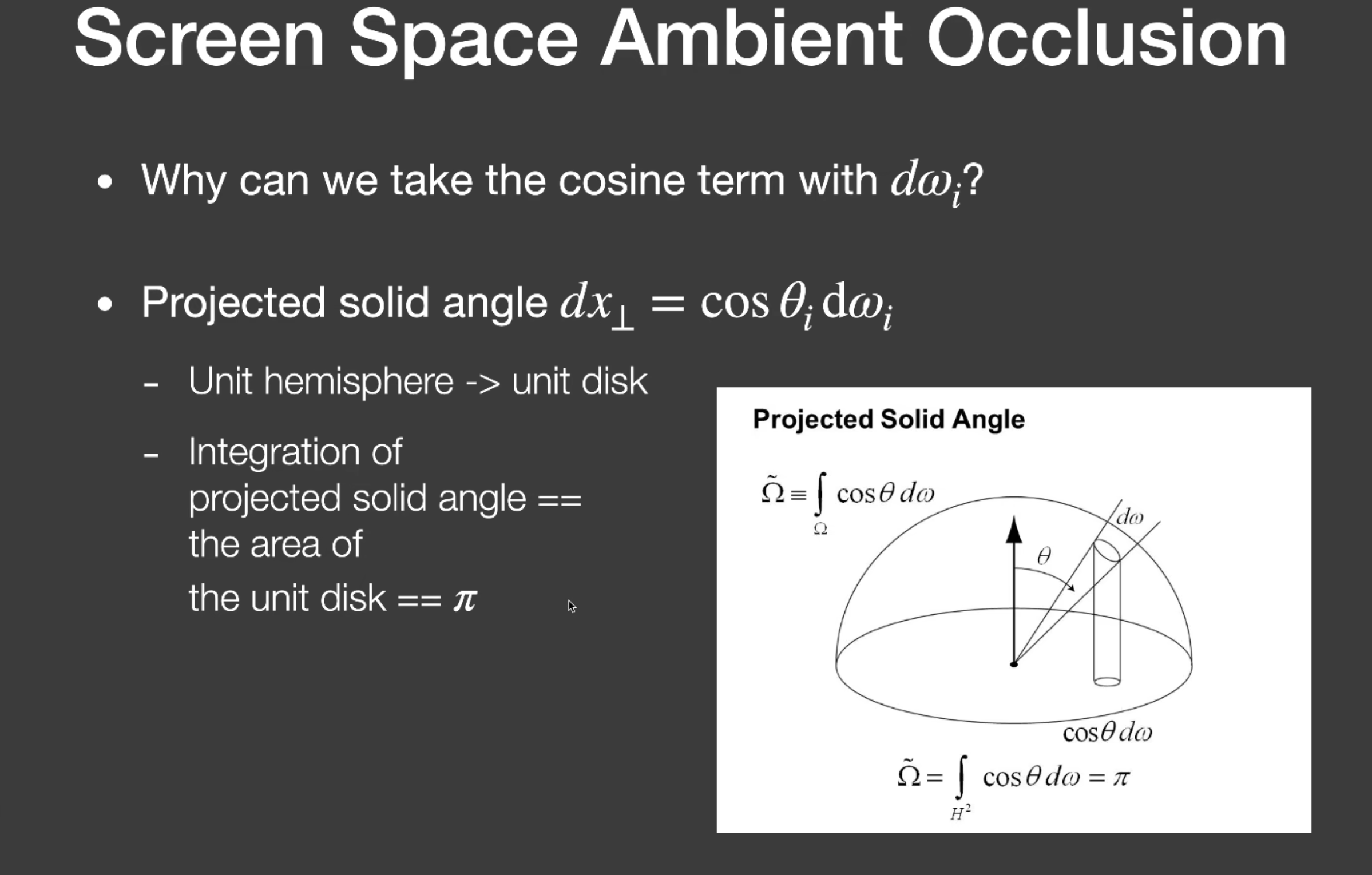
因为假设了环境光为常数，BRDF为常数，可以拿到积分外面

SSAO的做法

只考虑着色点附近半径为R的半球范围内的遮挡情况，这个R的选取可能会造成一些trick

SSAO进一步简化，用已经分布好的点来采样，然后算一个在物体外部的点数量比例。但是内外也不好算，再进一步假设用点深度比ShadingPoint深度近的来当作在物体外的点（会出现第二个点那种误判，不过出现概率不过所以没关系）。这里没有画出来，但是实际使用的法线方向的半球来采样的。

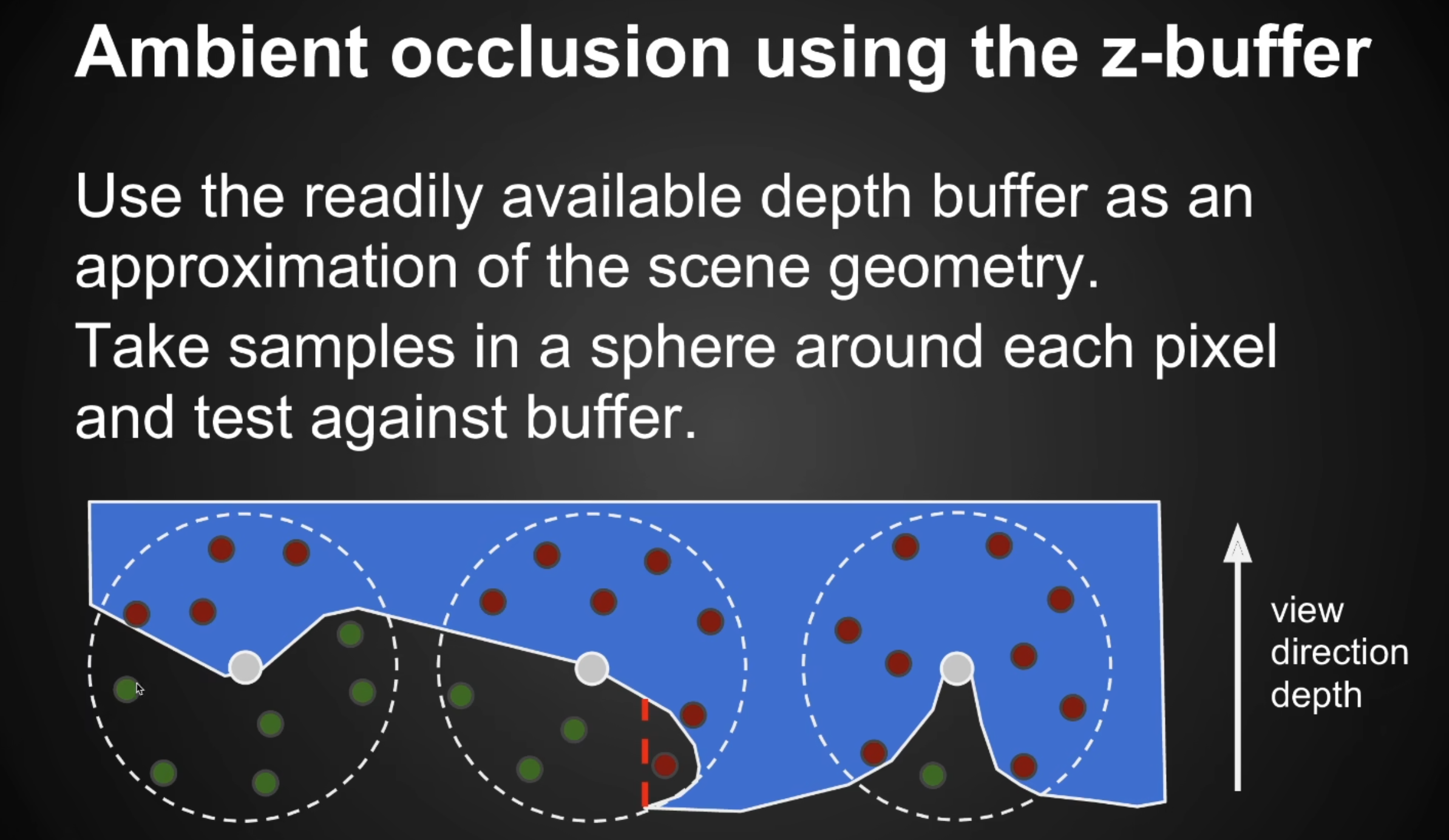
SSAO的问题：

没有考虑空间连续性，在前后没有连续的石凳附近也出现了AO。SSAO的理论本来是用R半径限制的，但是为了实现更快又假设用深度来比较了，这里相当于丢了深度方向的距离R这个条件（相当于在深度图上只考虑了2维的R半径）。

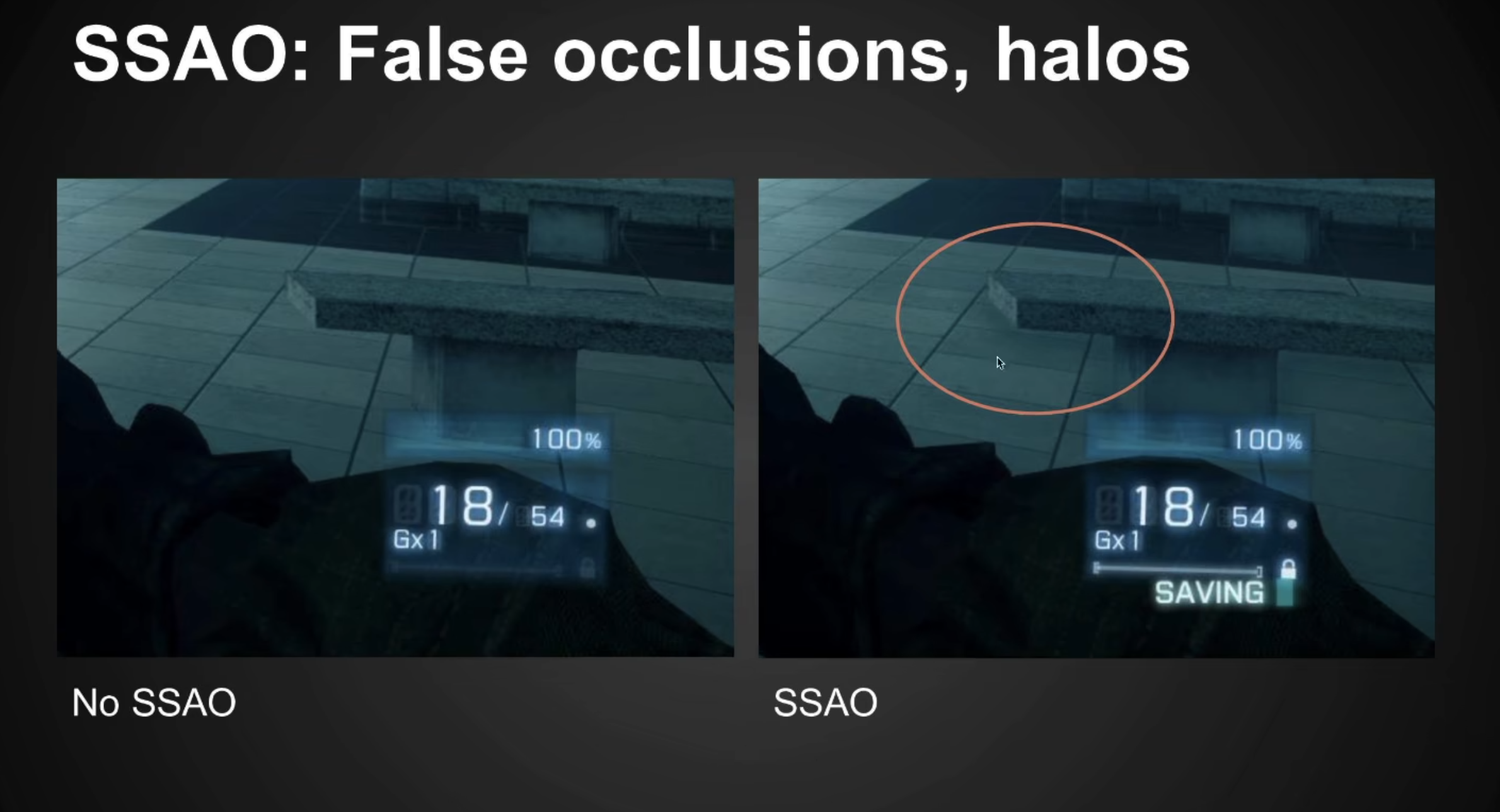
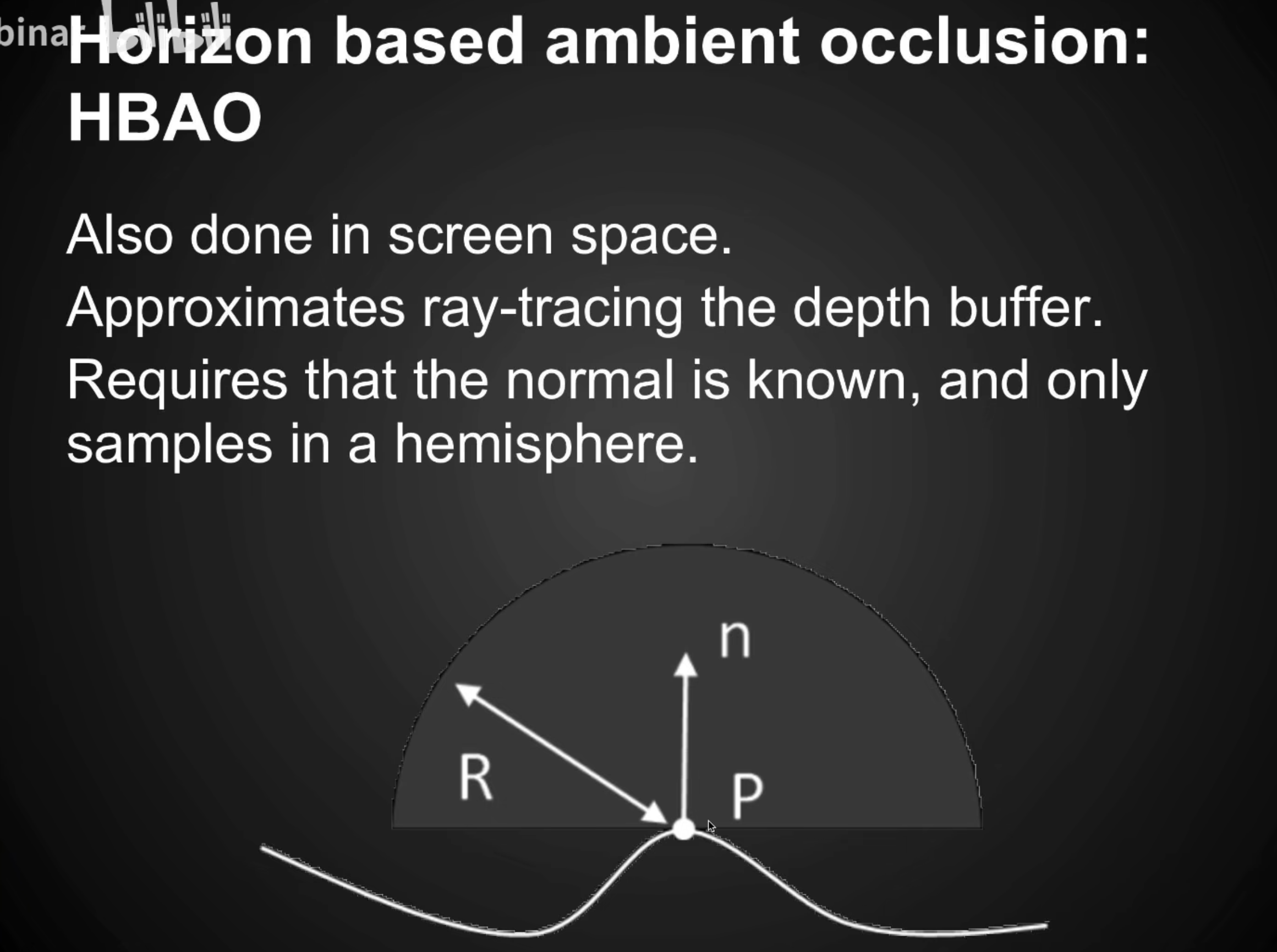
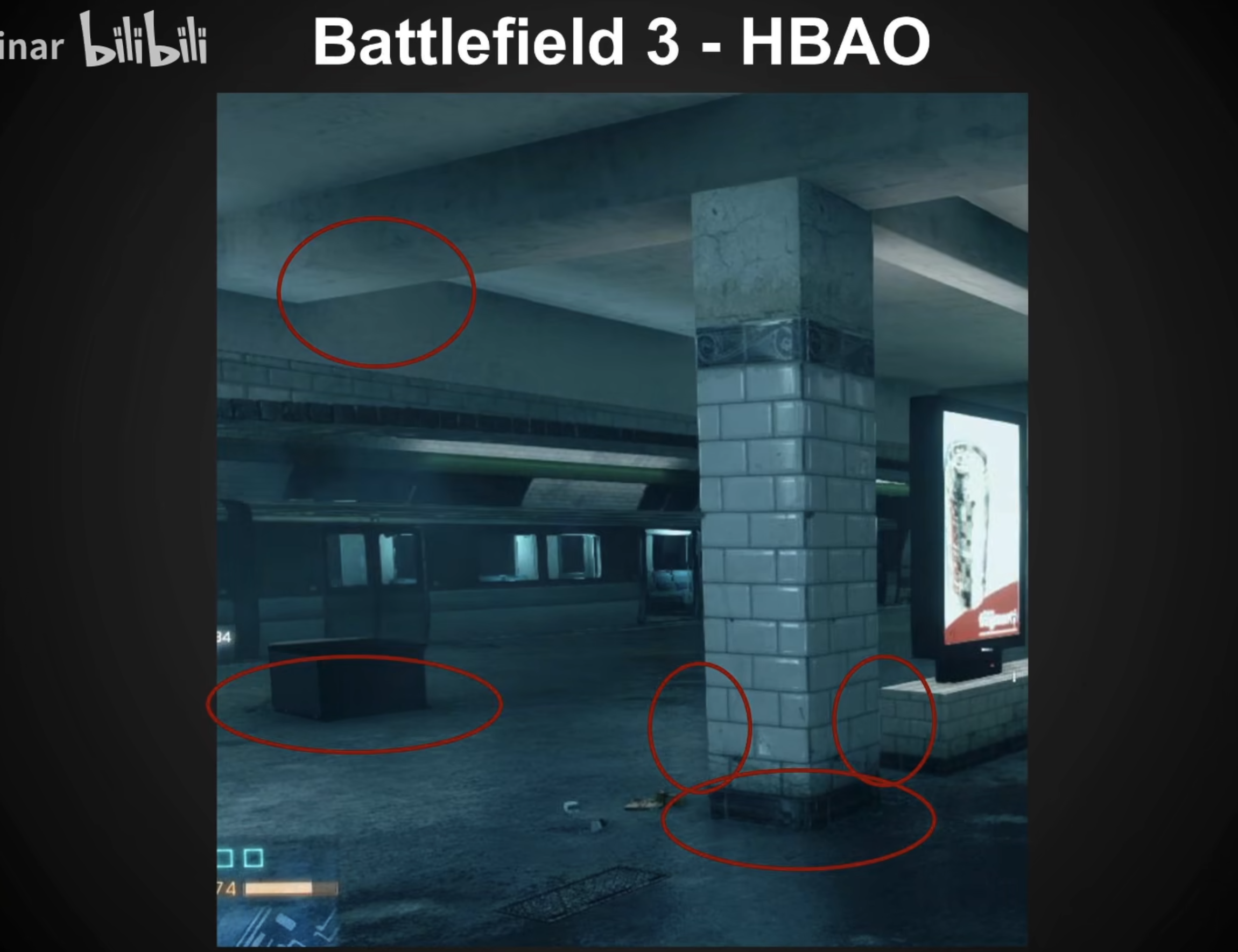
可以用HBAO来解决（会真正考虑一个半球范围）