
Games202-lecture4-实时阴影2
本节大纲

PCF和PCSS深入理解
PCF的数学原理:卷积(加权平均)
PCSS本质是比较场景深度和深度图上周围像素比较,即PCF的工作,PCSS主要就是在深度图上周围像素这个size会变换。
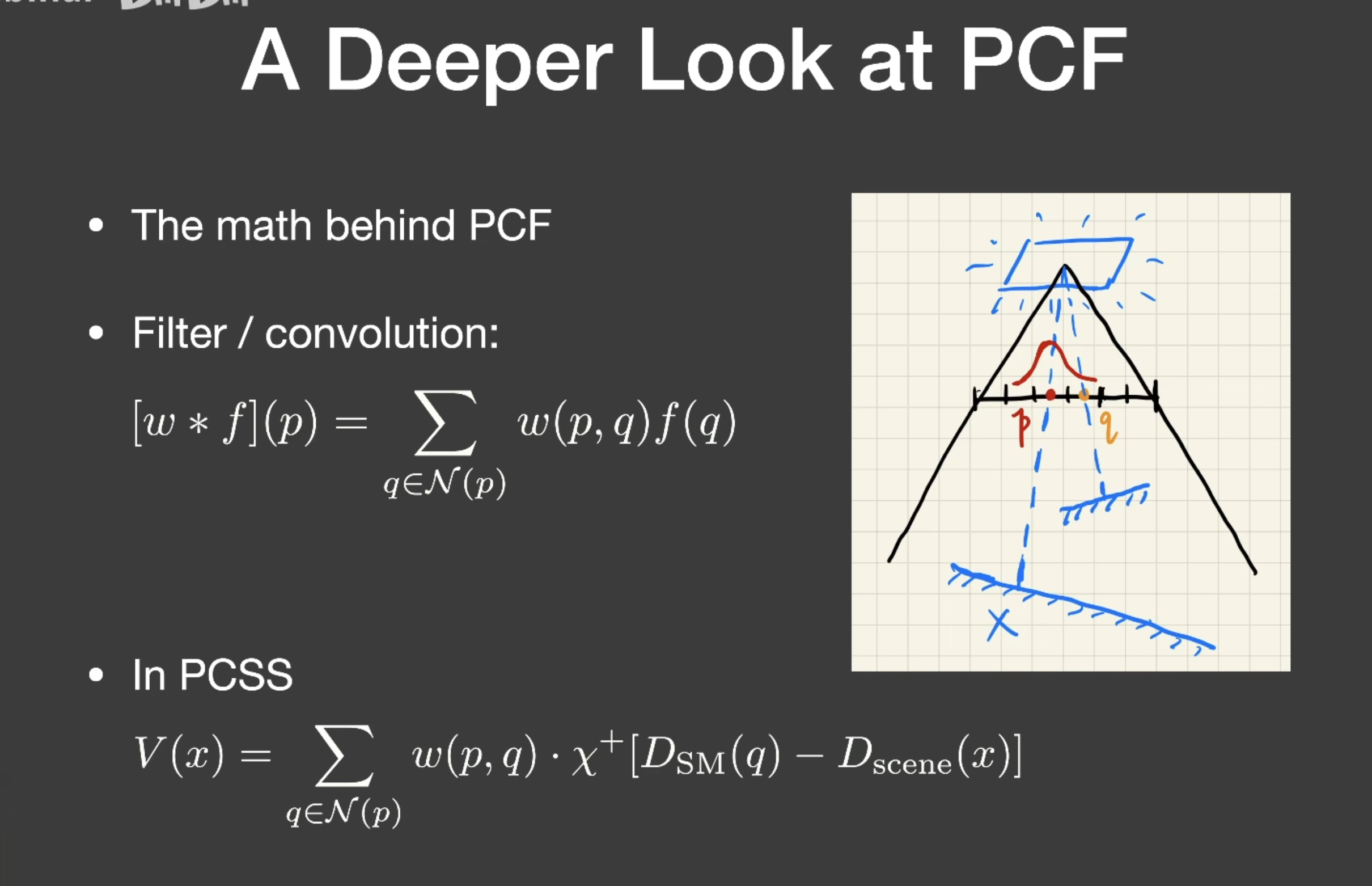
深度图上卷积再比较与深度比较后再卷积的区别

回顾一下PCSS,主要是性能问题(第一步是求遮挡物的平均深度)

Variance Soft Shadow Mapping (VSSM)
主要是加速PCSS的第一步和第三步

先假设深度都是正态分布的,那么只需要通过方差和均值就可以近似求得当前像素的百分比
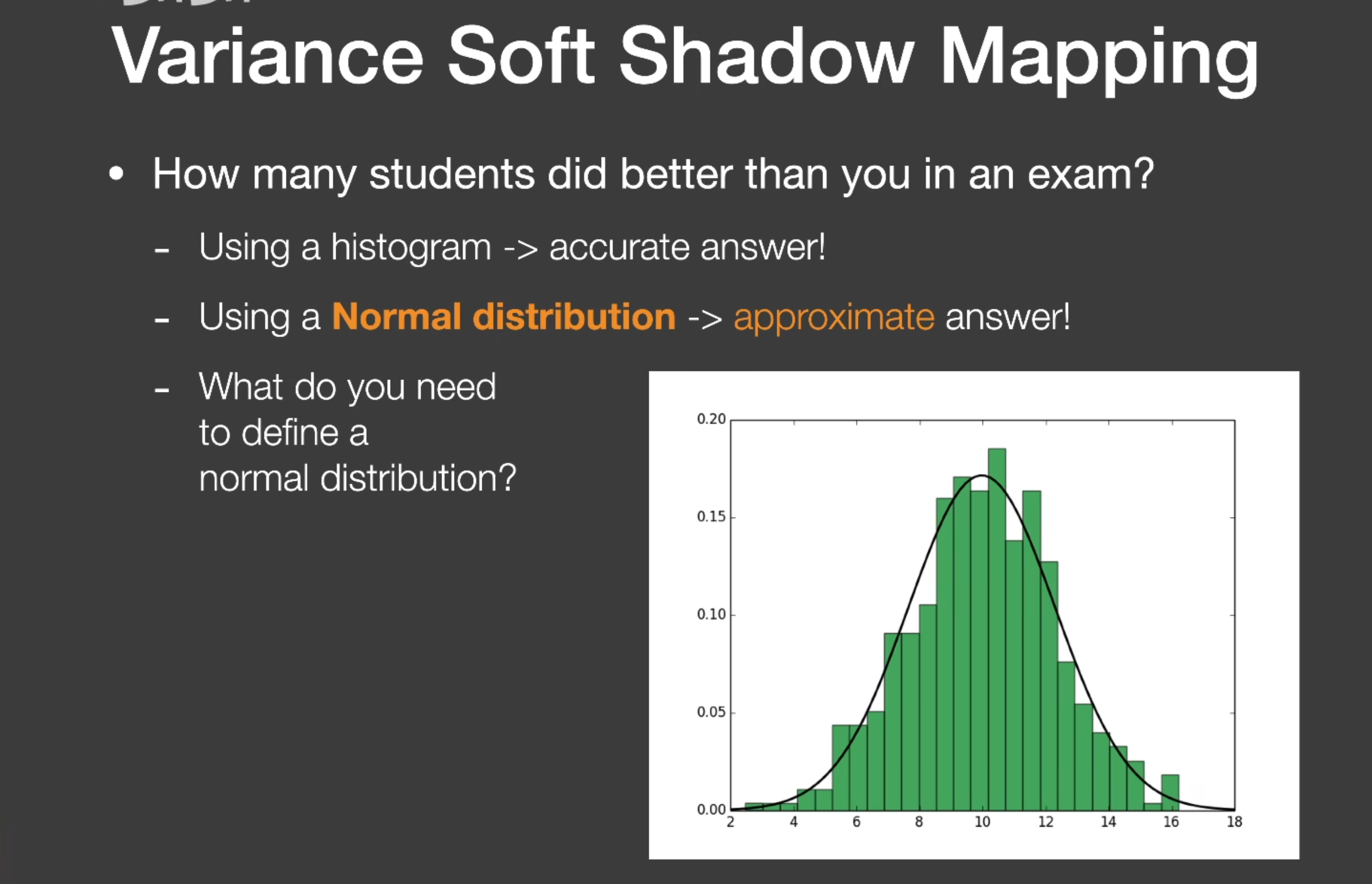
求深度在某一块的均值和方差可以通过深度和深度平方的图(一张图可以用rg储存)来求得

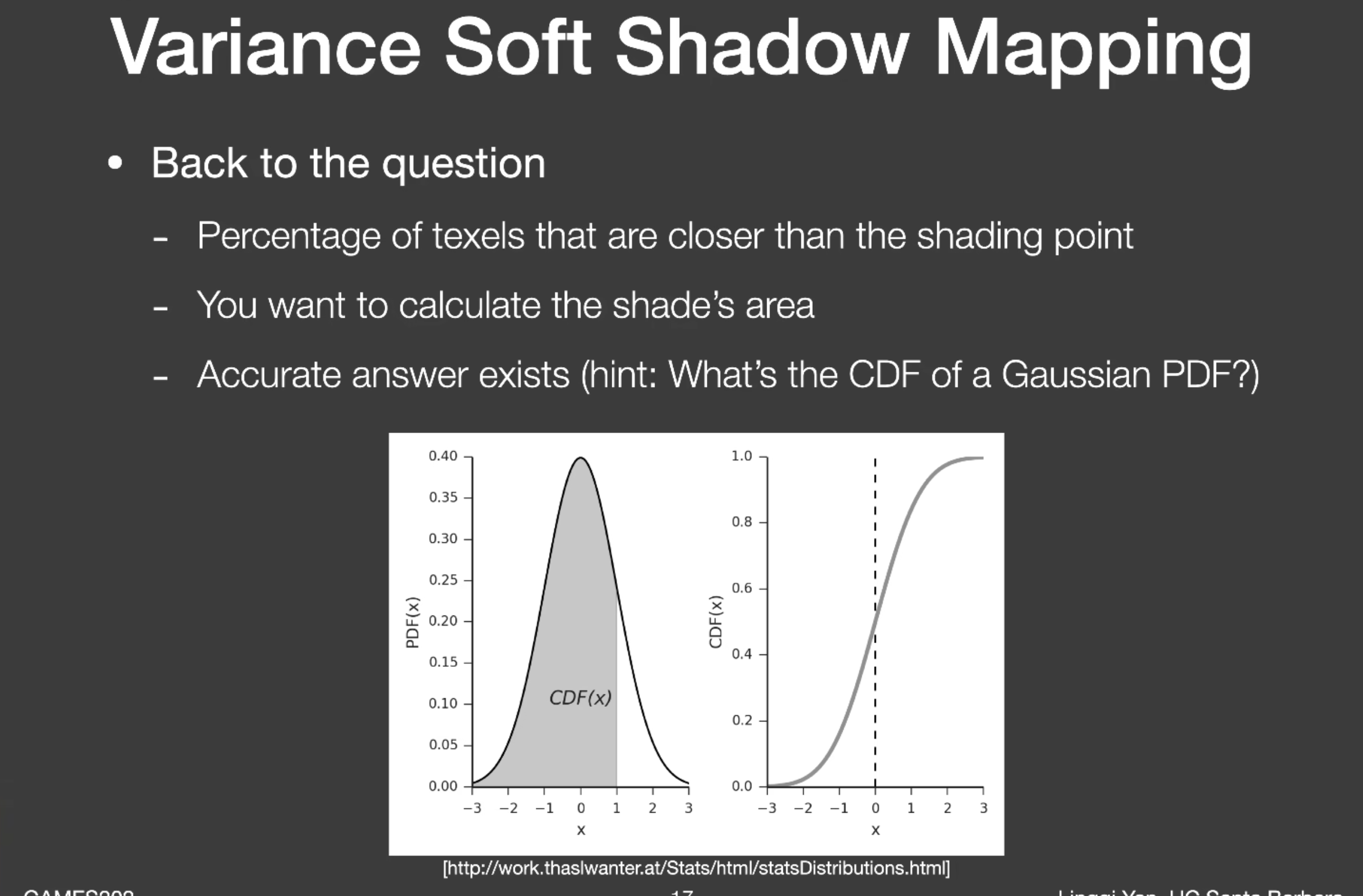
求CDF需要打表,或者用c++解析解的函数求得
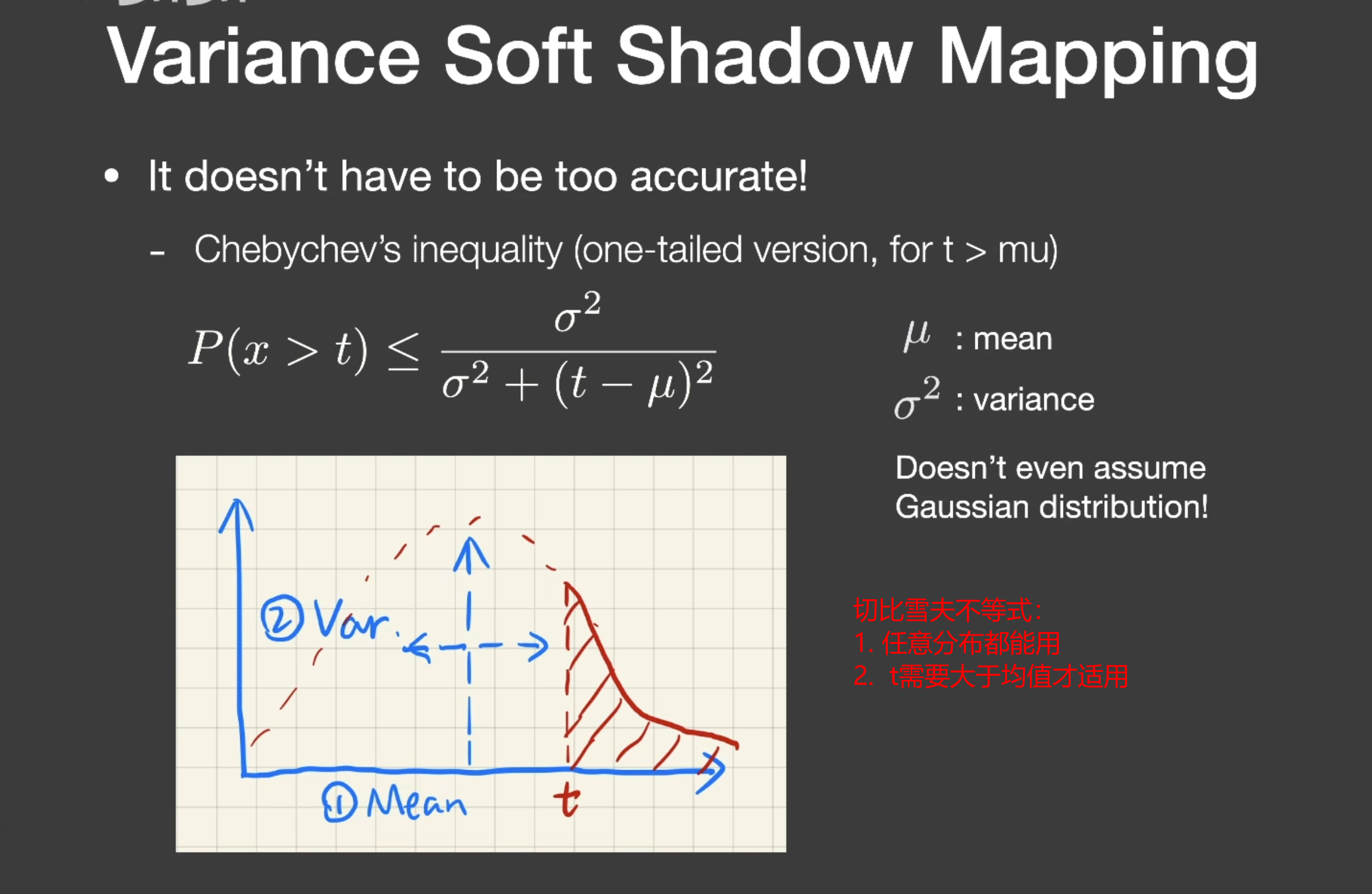
又假设切比雪夫不等式来优化计算CDF时间:这里把不等式假设为等式,t的限制也不考虑了,CDF = 1 - P(x)
第三步的深度平均值好算,但是第一步需要的是遮挡物的平均深度不好做:这里直接假设非遮挡物的平均深度为t,这样就可以解出来遮挡物的平均深度了

VSSM的效果

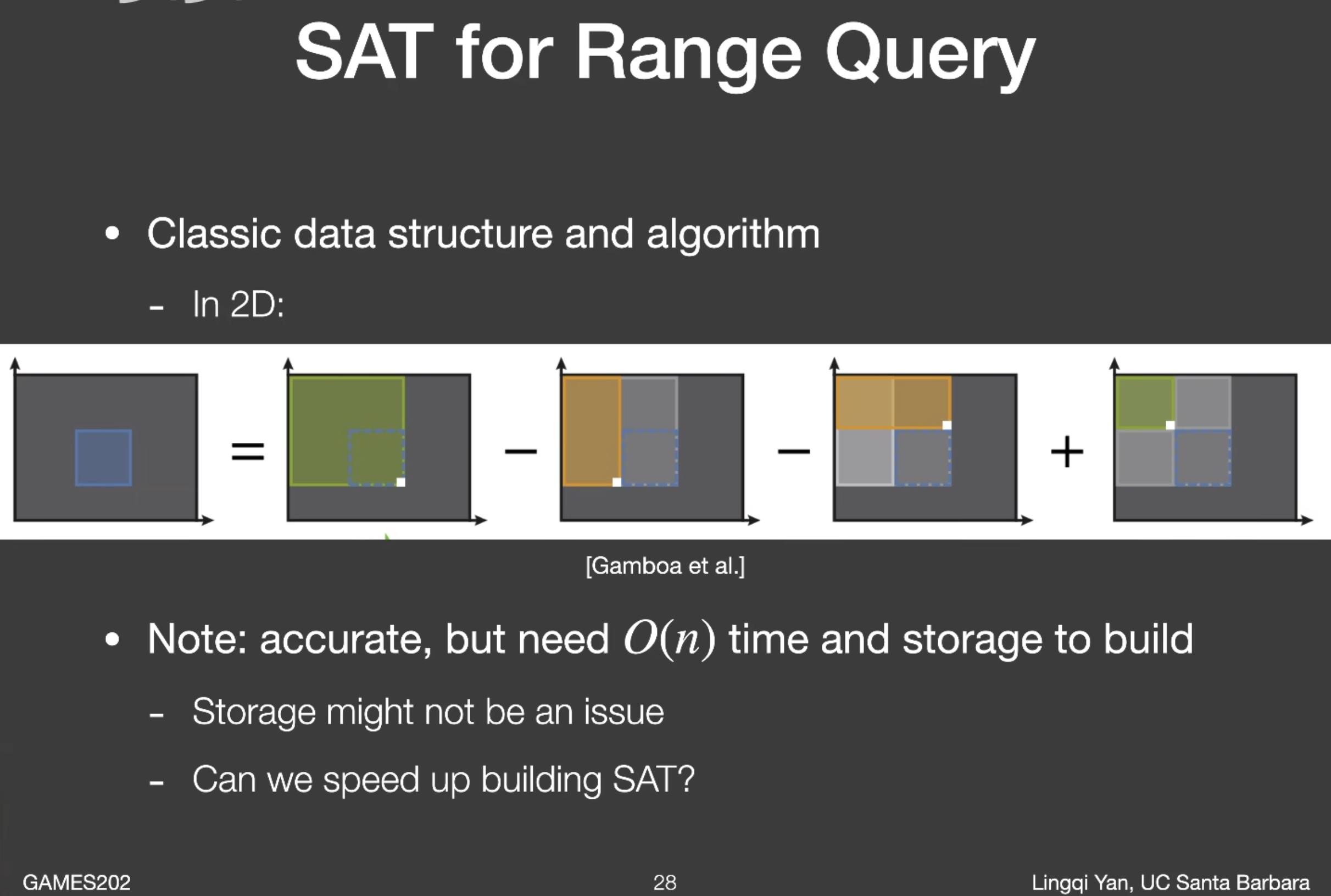
深度图的Mipmap怎么做:Summed Area Table(SAT)
一定范围内求平均或者一定范围内求总和(前缀和算法)
一维情况:SAT的值为加到当前索引i的和,算3到6的总和直接用SAT[6] - SAT[3]就能得到

二维情况:SAT表示从左上角加到当前位置的值(做法:横着加一遍,再竖着加一遍)
Moment Shadow mapping
VSSM的问题:比较杂乱的情况下效果还不错,但是简单情况就容易露馅(变白:本来应该有阴影的红色框的阴影却不明显,变黑:本来不该有阴影的地方却变成了阴影)
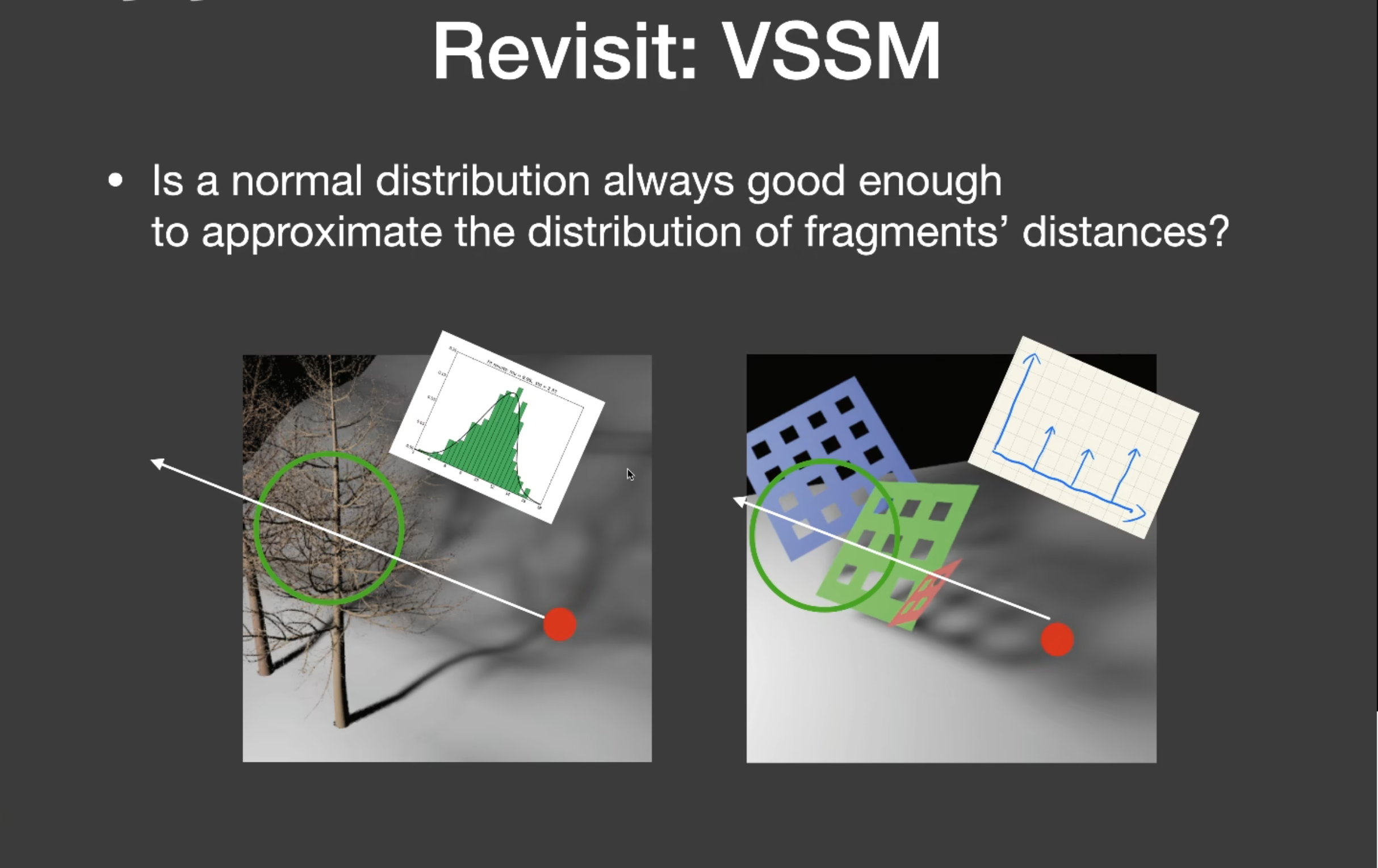

Moment Shadow Mapping解决VSSM分布不准的问题:Moment(矩),这里可以用高级的矩来描述分布(VSSM等效于只用到了x和x^2,也就是二阶矩)

理论的来源:4阶矩模拟PCF就挺准了(用一张rgbaHalf的图来储存)
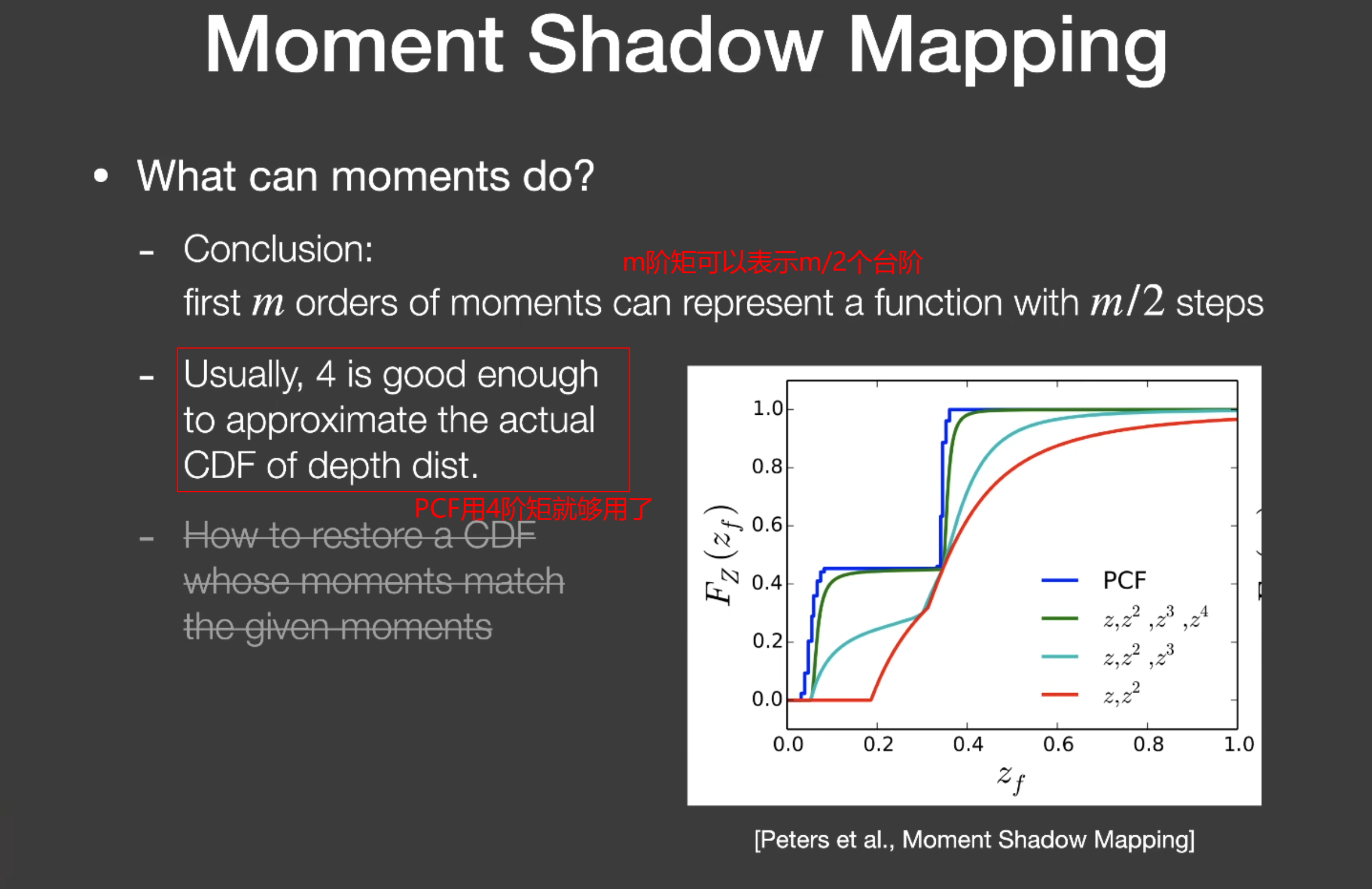
Moment Shadow Mapping的效果
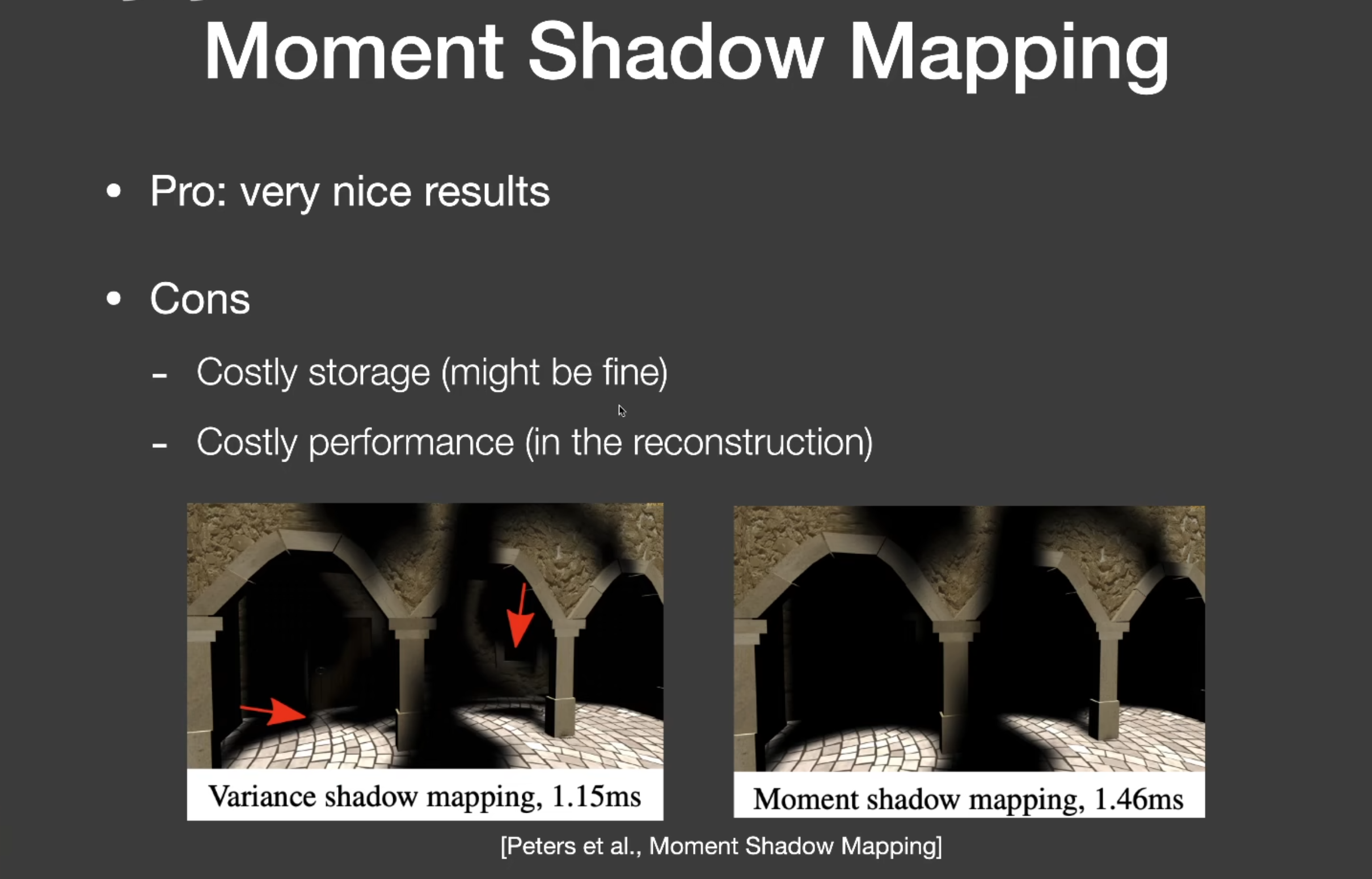
Moment的解法公式较为复杂:
MOIT的矩用法

M OIT中的解法
这里先假设bj(bj可以为其它z^j的函数)为z的j次方,先求出q这个向量的值
MOIT这里的bj相当于是还乘上了log(alpha),貌似这里的矩bj应该是某一块的z平均值
然后解一个一元m/2次的方程,解出m/2个解zi(不包括z0)
比较zi和z0的大小,得出vl,即v矩阵
再解矩阵的得到向量u
最后把bj*uj求和
MSM中矩的用法

MSM中的解法
引用
- 标题: Games202-lecture4-实时阴影2
- 作者: Zh-Hui
- 创建于 : 2025-01-21 22:32:51
- 更新于 : 2025-03-23 00:31:34
- 链接: https://hui1520.top/2025/01/21/Games202-lecture4/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论